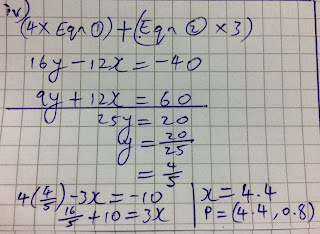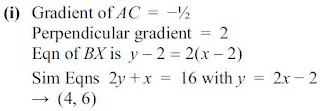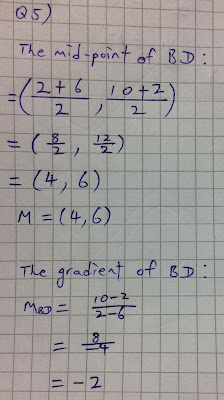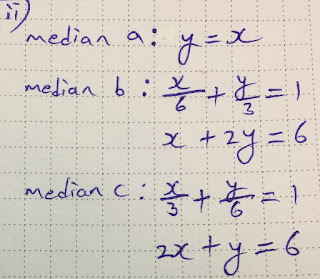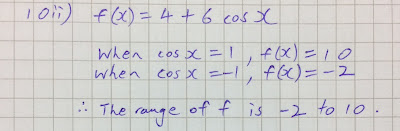You are given the co-ordinates of the four points A(6, 2), B(2, 4), C(−6, −2) and D(−2, −4).

You are given the co-ordinates of the four points A(6, 2), B(2, 4), C(−6, −2) and D(−2, −4).

(i) Calculate the gradients of the lines AB, CB, DC and DA.
Hence describe the shape of the figure ABCD.

(ii) Show that the equation of the line DA is 4y − 3x = −10 and find the length DA.

(iii) Calculate the gradient of a line which is perpendicular to DA and hence find the equation of the line l through B which is perpendicular to DA.

(iv) Calculate the co-ordinates of the point P where l meets DA.

(v) Calculate the area of the figure ABCD.

Solution:

The diagram shows a triangle whose vertices are A(−2, 1), B(1, 7) and C(3, 1).

The diagram shows a triangle whose vertices are A(−2, 1), B(1, 7) and C(3, 1).
The point L is the foot of the perpendicular from A to BC, and M is the foot of
the perpendicular from B to AC.
(i) Find the gradient of the line BC.
(ii) Find the equation of the line AL.
(iii) Write down the equation of the line BM.

Solution:

9709/MayJune/1/2008/Q11

In the diagram, the points A and C lie on the x- and y-axes respectively and the equation of AC is
2y + x = 16. The point B has coordinates (2, 2). The perpendicular from B to AC meets AC at the
point X.
(i) Find the coordinates of X. [4]
The point D is such that the quadrilateral ABCD has AC as a line of symmetry.
(ii) Find the coordinates of D. [2]
(iii) Find, correct to 1 decimal place, the perimeter of ABCD. [3]

Solution:

(ii)

D = (6,10)

(iii)

Reference: PYQ - May/June 2008 Paper 1 Q11

9709/MayJune/1/2005/Q5

The diagram shows a rhombus ABCD. The points B and D have coordinates (2, 10) and (6, 2) respectively, and A lies on the x-axis. The mid-point of BD isM. Find, by calculation, the coordinates of each of M, A and C.

Solution:

Reference: PYQ - May/June 2005 Paper 1 Q5

A median of a triangle is a line joining one of the vertices to the mid-point of the opposite side.

A median of a triangle is a line joining one of the vertices to the mid-point of
the opposite side.

In a triangle OAB, O is at the origin, A is the point (0, 6) and B is the point (6, 0).

(i) Sketch the triangle.
(ii) Find the equations of the three medians of the triangle.
(iii) Show that the point (2, 2) lies on all three medians. (This shows that the medians of this triangle are concurrent.)

Solution:

9709/MayJune/13/2010/Q3

The function f : x  → a + b cos x is defined for 0 ≤ x ≤ 2pi. Given that f(0) = 10 and that f(2/3 pi) = 1, find
(i) the values of a and b, [2]
(ii) the range of f, [1]
(iii) the exact value of f(5/6  pi).  [2]

Solution:
i)

ii)

iii)

Reference: PYQ - May/June 2010 Paper 13 Q3

9709/MayJune/12/2010/Q11

The function f : x → 4 − 3 sin x is defined for the domain 0 ≤ x ≤ 2pi.

(i) Solve the equation f(x) = 2. [3]

(ii) Sketch the graph of y = f(x). [2]

(iii) Find the set of values of k for which the equation f(x) = k has no solution. [2]

The function g : x → 4 − 3 sin x is defined for the domain 1/2 ≤ x ≤ A

(iv) State the largest value of A for which g has an inverse. [1]

(v) For this value of A, find the value of g⁻¹(3). [2]

Solution:

i)

ii)

f(x) = 3 sin x

f(x) = -3 sin x

f(x) = 4 - 3 sin x

iii)

iv)

v)

Reference: PYQ - May/June 2010 Paper 12 Q11