9709/Oct Nov/2005/3/Q9

(i)  Express (3x^2 + x) / (x + 2)(x^2 + 1) in partial fractions.
(ii) Hence obtain the expansion of (3x^2 + x) / (x + 2)(x^2 + 1) in ascending powers of x, up to and including the term in x^3.

Solution:

Reference: PYQ - Oct/Nov 2005 Paper 3 Q9

9709/Oct Nov/2009/32/Q6

6i) Use the substitution x = 2 tan q to show that

6ii) Hence find the exact value of

Solution:

Reference: PYQ - Oct/Nov 2009 Paper 32 Q6

Add caption

9709/Oct Nov/2003/4/Q6

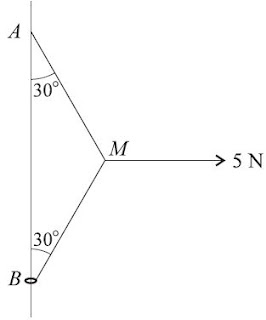
One end of a light inextensible string is attached to a fixed point A of a fixed vertical wire. The other end of the string is attached to a small ring B, of mass 0.2 kg, through which the wire passes.

A horizontal force of magnitude 5N is applied to the mid-point M of the string. The system is in equilibrium with the string taut, with B below A, and with angles ABM and BAM equal to 30◦ (see diagram).

(i) Show that the tension in BM is 5N.

(ii) The ring is on the point of sliding up the wire. Find the coefficient of friction between the ring and the wire.

(iii) A particle of mass m kg is attached to the ring. The ring is now on the point of sliding down the wire. Given that the coefficient of friction between the ring and the wire is unchanged, find the value of m.

Solution:

Reference: PYQ - Oct/Nov 2003 Paper 4 Q6

9709/Oct Nov/2003/4/Q5

Particles A and B, of masses 0.4 kg and 0.1 kg respectively, are attached to the ends of a light inextensible string. Particle A is held at rest on a horizontal table with the string passing over a smooth pulley at the edge of the table. Particle B hangs vertically below the pulley (see diagram). The system is released from rest. In the subsequent motion a constant frictional force of magnitude 0.6N acts on A. Find

(i) the tension in the string, 

(ii) the speed of B 1.5 s after it starts to move.

Solution:

 
Reference: PYQ - Oct/Nov 2003 Paper 4 Q5

9709/May Jun/2003/4/Q5

S₁ and S₂ are light inextensible strings, and A and B are particles each of mass 0.2 kg. Particle A is suspended from a fixed point O by the string S₁, and particle B is suspended from A by the string S₂.

The particles hang in equilibrium as shown in the diagram.

(i) Find the tensions in S₁ and S₂.

The string S₁ is cut and the particles fall. The air resistance acting on A is 0.4N and the air resistance acting on B is 0.2N.

(ii) Find the acceleration of the particles and the tension in S₂.

Solution:

Reference: PYQ - May/June 2003 Paper 4 Q5

9709/Oct Nov/2002/4/Q7

A particle P starts to move from a point O and travels in a straight line. At time ts after P starts to

move its velocity is v ms^-1, where v - 0.12t - 0.0006t².

(i) Verify that P comes to instantaneous rest when t = 200, and find the acceleration with which it

starts to return towards O.

(ii) Find the maximum speed of P for 0 <= t <= 200.

(iii) Find the displacement of P from O when t = 200.

(iv) Find the value of t when P reaches O again.

Solution:

 

Reference: PYQ - Oct/Nov 2002 Paper 4 Q7

9709/Oct Nov/2002/4/Q4

Two particles A and B are projected vertically upwards from horizontal ground at the same instant.

The speeds of projection of A and B are 5ms^-1 and 8ms^-1 respectively. Find

(i) the difference in the heights of A and B when A is at its maximum height,

(ii) the height of A above the ground when B is 0.9m above A.

Solution:

Reference: PYQ - Oct/Nov 2002 Paper 4 Q4

9709/Oct Nov/2002/4/Q3

A light inextensible string has its ends attached to two fixed points A and B, with A vertically above B. A smooth ring R, of mass 0.8 kg, is threaded on the string and is pulled by a horizontal force of magnitude X newtons. The sections AR and BR of the string make angles of 50^o and 20^o  respectively with the horizontal, as shown in the diagram. The ring rests in equilibrium with the string taut. Find

(i) the tension in the string,

(ii) the value of X.

Solution:

Reference: PYQ - Oct/Nov 2002 Paper 4 Q3

Integration Question 24

Integrate e^2x cos x

Solution:

Integration Question 15 and Question 20

a) Integrate x^m ln x
b) Integrate x^1/2 ln x

Solution: